This post will discuss three types of uncertainty and how they can be used to understand cryptography. According to Wikipedia, uncertainty refers to an incomplete and/or unknown piece of information. A prediction is an estimate of what will occur in the future, an estimate of what has already been measured or an estimate of what is yet to be measured.

This post will discuss three types of uncertainty and how they can be used to understand cryptography. According to Wikipedia, uncertainty refers to an incomplete and/or unknown piece of information.
A prediction is an estimate of what will occur in the future, an estimate of what has already been measured or an estimate of what is yet to be measured.
Here, we need to consider two main concepts: information and knowledge. Uncertainty can be defined as a lack of information or knowledge. As we’ll see, these two concepts are not equivalent and do not cover every situation. In order to understand uncertainty, we need to start at the strongest level.
Ontological Uncertainty: Indeterminacy

The Bloch sphere representing the state of a spin 1/2 particle.
As described in quantum mechanics, certain particles (spin 1/2 particles like electrons) have a property called spin that gives two discrete results, called “spin up” and “spin down”. The equation below describes this.
As a result, the probability of getting spin up equals α, and the probability of getting spin down equalsβ².
If we were to measure the spin before we measured it, would it be up or down? The equation above, however, only gives us probabilities for what will happen when we measure. We might ask ourselves, before we measure it, is the spin up or down? But the equation above only gives us probabilities of what will happen when we make the measurement.
According to mainstream interpretations of quantum mechanics, we cannot know what the spin value was before the measurement. Furthermore, it is impossible to predict what the measurement will reveal before it occurs. Our question requires information that presently doesn’t exist.
As a result of this intrinsic indeterminacy, we use the term ontological uncertainty: uncertainty is not a property of knowledge, but one of nature. Our confusion results from an ontological mismatch between nature and our models of it. This type of uncertainty can be summarized as follows:
We cannot know the information because it does not exist.
As a side note, the Heisenberg uncertainty principle is not very well named, since it is similar to the subject of the next section. The indeterminacy principle would be a better name.
Information Deficit: Epistemic Uncertainty
We began with the strongest and strangest form of uncertainty. The second type is encountered when dealing with incomplete information every day. Unlike the previous type of uncertainty, this uncertainty is a property of our state of knowledge, not of nature. For example, when we ask what caused dinosaur extinction, we are referring to a fact about reality, no matter how accessible it may be. In poker, when we wonder whether we have the best hand, we are referring to an unknown but existing fact, the set of all hands dealt.
In fields such as information theory, probability, and thermodynamics, uncertainty is treated as incomplete information. The technical term is entropy, and it’s measured in bits. If a description lacks a lot of information, it is said to have high entropy. In asking whether the coin will land heads or tails, we are missing one bit of information. Three bits are missing if we ask what number will come out of a fair 8-sided die. There are more possibilities in a die throw than in a coin flip, so there is a higher degree of uncertainty about the outcome. As a result, it has more entropy bits. This type of uncertainty can be summarized as follows:
We do not know the information, but it exists.
Before I finish, I would like to clarify a few things. Here’s the reason why the concept of randomness didn’t appear when discussing coin flips and die rolls. This section discusses classical physics, where phenomena are deterministic even if we don’t know all of the initial conditions. There is a combination of determinism and unknown initial conditions that underlies the use of randomness at the macroscale. Subjective randomness is sometimes used to distinguish it from intrinsic randomness, which is an alternative term for ontological uncertainty.

A deterministic coin flipping machine
The Third Type…
Now for the interesting part. Imagine I have all the information about something, but I still don’t know everything about it. Sounds contradictory right? Here’s an example to illustrate this kind of situation.
- All men are mortal
- Socrates is a man
If now somebody tells you that
- Socrates is mortal.
Are they giving you any information? Hopefully it seems to you like they told you something you already knew. Was there any information prior to giving statement 3? Put differently, does statement 3 contain any information not present in 1,2?
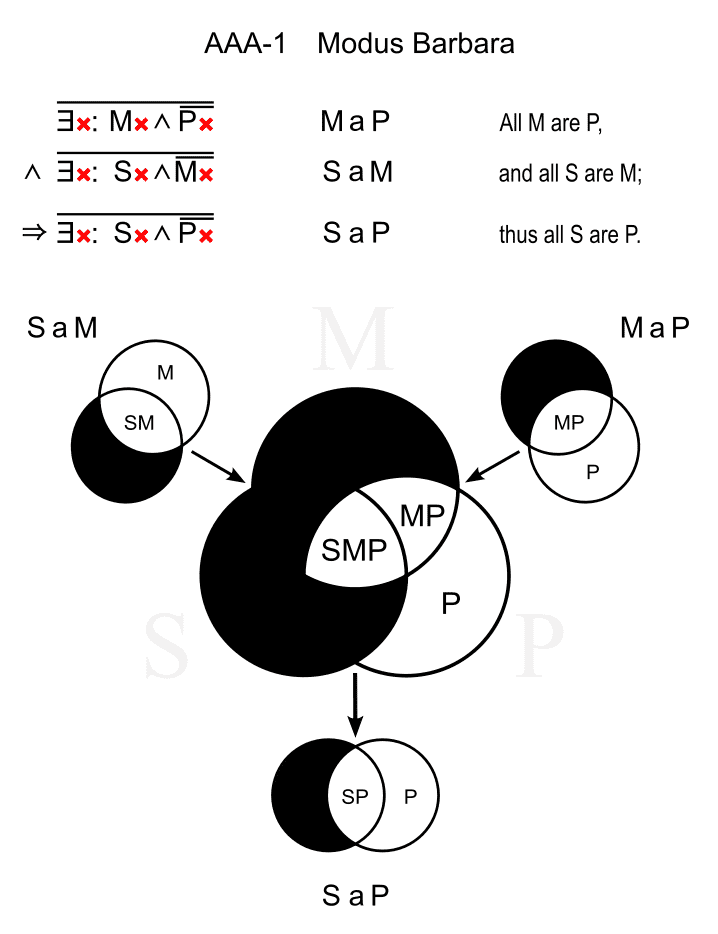
One of the 24 valid syllogism types
Consider another example.
- x = 1051
- y = 3067
- x * y = 3223417
In this case statement 3 tells us something we probably didn’t know. But does statement 3 contain information not present in 1 and 2? We can turn to definitions from information theory in order to provide an answer. Define three random variables (for convenience in some arbitrary range a-b)
x ∈ {a-b}, y ∈ {a-b}, x*y {…}
We can calculate the conditional entropy according to the standard equation which in our case gives
H(x*y | x, y) = 0
The conditional entropy of xy given x and y is zero. This is simply a technical way to say that given statements 1 and 2, statement 3 contains no extra information: whatever 3 tells us was already contained in 1,2. Once x and y are fixed, xy follows necessarily. This brings us back to the beginning of the post.
We could say that uncertainty is lack of knowledge or even lack of information. As we’ll see, these two ideas are not equivalent and cannot be applied to every situation.
The two ideas differ now, as should be evident. In this case, we have all the information about something (x, y), but we do not know everything about it (x*y).
Logical Uncertainty: Computation Deficit
It is computation that bridges having all the information with having all the knowledge. In the Socrates syllogism, deducing (computing) the conclusion from the premises adds no information. A calculation based on x and y does not produce an answer. Despite the fact that the information was always there, computation can tell us things we did not know.

We are uncertain about the blanks, even though we have all the necessary information to fill them.
The goal of computing is to derive implicit consequences from data. The distinction between deducing the conclusion of a simple syllogism and multiplying two large numbers is one of degree, not kind. There is a clear difference, however, in that without sufficient computation, we will remain uncertain about things that are already present. At the high end, there are cases such as Fermat’s last theorem, about which mathematicians have been unsure for 350 years. We conclude with a summary of logical uncertainty:
We have all of the information, but there are logical consequences we are unaware of.

Pierre de Fermat
Cryptography: Secrecy and Uncertainty
Cryptography (from Greek kryptós, “hidden, secret,” and v graphein, “writing”) is the practice and study of secure communication techniques in the presence of third parties known as adversaries.
The key word here is “secret,” which should remind us of our uncertainty. To say that we want a message to remain secret from an adversary is to say that we want this adversary to be unsure about the message’s content. Although our first instinct would lead us to believe that epistemic uncertainty exists, this is not always the case.
Consider the Caesar cipher, named after Julius Caesar, who used it over 2000 years ago. Each letter in the message is replaced by another letter obtained by shifting the alphabet a fixed number of places. This number of locations serves as the encryption key. For example, with a +3 shift
abcdefghijklmnopqrstuvwxyz defghijklmnopqrstuvwxyzabc
Let’s encrypt a message using this +3 key:
cryptography is based on uncertainty fubswrjudskb lv edvhg rq xqfhuwdlqwb
We hope that if our adversary obtains the encrypted message, he/she will not discover its secret, whereas our intended recipient, knowing the +3 shift key, can recover it by using the reverse procedure (-3 shift). When analyzing ciphers, we assume that our adversary will intercept our messages and will also know the procedure, if not the key (in this case +3) used to encrypt them. Assume we are the adversary and capture this encrypted message using these assumptions:
govv nyxo iye rkfo pyexn dro combod
We want to know the secret, but we don’t know what key shift value it is. However, because the alphabet has 26 characters, there are only 25 possible shifts; a shift of 26 leaves the message unchanged. So, why not try all of the keys and see what happens:
FNUU MXWN HXD QJEN OXDWM CQN BNLANC EMTT LWVM GWC PIDM NWCVL BPM AMKZMB DLSS KVUL FVB OHCL MVBUK AOL ZLJYLA CKRR JUTK EUA NGBK LUATJ ZNK YKIXKZ BJQQ ITSJ DTZ MFAJ KTZSI YMJ XJHWJY AIPP HSRI CSY LEZI JSYRH XLI WIGVIX ZHOO GRQH BRX KDYH IRXQG WKH VHFUHW YGNN FQPG AQW JCXG HQWPF VJG UGETGV XFMM EPOF ZPV IBWF GPVOE UIF TFDSFU WELL DONE YOU HAVE FOUND THE SECRET VDKK CNMD XNT GZUD ENTMC SGD RDBQDS UCJJ BMLC WMS FYTC DMSLB RFC QCAPCR TBII ALKB VLR EXSB CLRKA QEB PBZOBQ SAHH ZKJA UKQ DWRA BKQJZ PDA OAYNAP RZGG YJIZ TJP CVQZ AJPIY OCZ NZXMZO QYFF XIHY SIO BUPY ZIOHX NBY MYWLYN PXEE WHGX RHN ATOX YHNGW MAX LXVKXM OWDD VGFW QGM ZSNW XGMFV LZW KWUJWL NVCC UFEV PFL YRMV WFLEU KYV JVTIVK MUBB TEDU OEK XQLU VEKDT JXU IUSHUJ LTAA SDCT NDJ WPKT UDJCS IWT HTRGTI KSZZ RCBS MCI VOJS TCIBR HVS GSQFSH JRYY QBAR LBH UNIR SBHAQ GUR FRPERG IQXX PAZQ KAG TMHQ RAGZP FTQ EQODQF HPWW OZYP JZF SLGP QZFYO ESP DPNCPE
When we tried a key shift of +10, we discovered the secret. Take note of how we were able to isolate the correct message when none of the other attempts yielded meaningful results. This is due to the fact that the space of possible keys is so limited that only one of them decrypts to a possible message. Technically, the key space and message space[2] are small enough in comparison to the length of the message that only one key is required to decrypt it. In terms of uncertainty, the following inequality[3] expresses this:
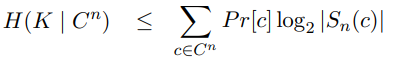
The left part of the expression, H(Key | Ciphertext), indicates how much uncertainty about the key remains once the encrypted message has been obtained. Take note of the term S(c), which represents the number of keys required to decrypt a meaningful message. As previously stated, S(c) = 1, resulting in H(K | C) = P(c) * log2 (1) = P(c) * 0 = 0.
In other words, once we know the encrypted message, there is no uncertainty about the key, and thus the secret message[4]. Of course, when we first captured this,
govv nyxo iye rkfo pyexn dro combod
We didn’t know the secret, but we had all the information we needed to find out. We were only logically uncertain about the secret and required computation rather than information to discover it.
Alberti’s cipher disk (1470)
Although we have only seen this for the simple Caesar cipher, it turns out that, with a large enough message to encrypt, many ciphers have this property. This is true for public key ciphers, such as those used in many secure voting systems, regardless of message size. Because our adversaries have enough information to obtain the secret, we can say that practical cryptography is based on logical uncertainty. However, as previously demonstrated, there are various degrees of logical uncertainty. Cryptography is based on this uncertainty being “strong” enough to keep secrets safe.
Talking about degrees of logical uncertainty leads us to computational complexity.
Logical Uncertainty and Computational Complexity
Computational complexity can be said to measure logical uncertainty in the same way that entropy measures epistemic uncertainty. In probability theory, we investigate how much information is required to eliminate epistemic uncertainty. Computational complexity is the amount of computation required to remove logical uncertainty. We saw that while deducing the conclusion of Socrates’ syllogism was simple, multiplying two large numbers was difficult. Complexity considers how difficult these problems are in comparison to one another. So, if we’re looking for the foundations of cryptography, we should start there.
Consider the widely used RSA public key cryptosystem. This scheme is based on the computational difficulty of factoring large numbers, among other things. This situation can be represented by two statements, for example:
- X=1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139
- X=3797522793694367392280887275544562785456553663 199*40094690950920881030683735292761468389214899724061
Statement 2 (the factors) is implied by statement 1, but obtaining 2 from 1 necessitates considerable computational effort. In practice, an adversary who intercepts a message encrypted with the RSA scheme will need so much computation to decrypt it that this possibility is labeled infeasible. Let’s be a little more specific. This means that an adversary will need thousands of years of computing time on a modern computer to complete the task using the fastest known algorithm.
If the previous statement did not set off alarm bells, perhaps I should emphasize the words “well-known algorithm.” We know that using known algorithms is impossible, but what if a faster algorithm is discovered? You’d think complexity theory would have a solution for that hypothetical situation. The simple truth is that it does not.
Problems for which efficient algorithms exist are classified as P in complexity theory. Although no efficient algorithm for integer factorization is known, whether it is in P or not is an open question[5]. In other words, we are logically unsure whether factorization occurs in P!
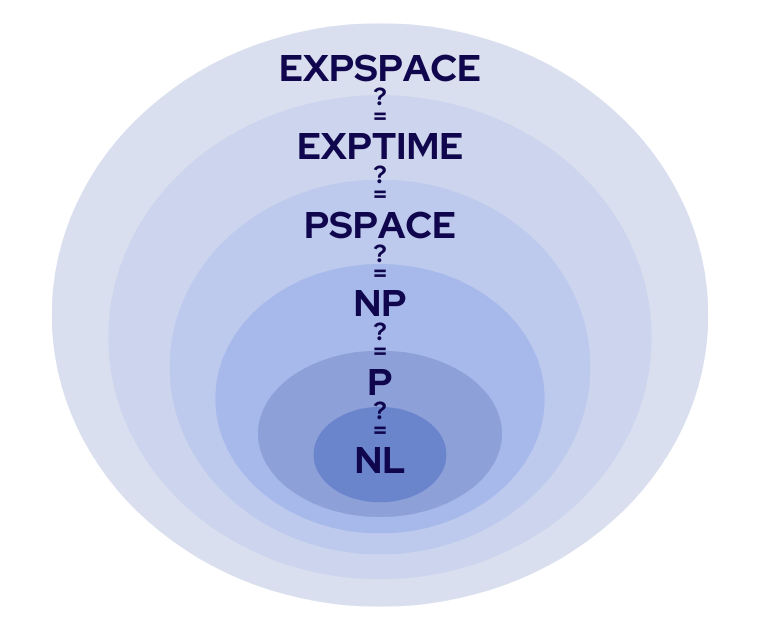
Several complexity classes
Assuming that integer factorization does not exist in P, a message encrypted with RSA is secure. To ensure an adversary’s logical uncertainty about secret messages, cryptographic techniques rely on assumptions that are the subject of logical uncertainty at the computational complexity level! Not what you want to find when looking for foundations.
In Conclusion
But it’s not all that bad. When you think about it, it’s not so much whether factorization and other problems are in P as it is whether adversaries will find the corresponding efficient algorithms. The condition that factorization is in P and that efficient algorithms are discovered secretly by adversaries is far more powerful than the first requirement alone. More importantly, the second condition appears to be one for which we can find some evidence.
It is debatable whether or not evidence can be found for a logical statement. Is the fact that no one has proven that factorization is in P evidence that it isn’t? Some say yes, while others say no. However, it appears less controversial to assert that the fact that no algorithm has been discovered serves as evidence for the possibility that we (as a species with a given level of cognitive and scientific advancement) will not discover it in the near future.

Several complexity classes
The bottom line for cryptography’s foundations is a matter of both logical and epistemic uncertainty. On the one hand, questions about computational complexity belong in the realm of logic, and empirical evidence for this appears conceptually shaky. However, the practical aspects of cryptography are dependent not only on complexity issues, but also on our ability to solve them. Another point to consider is that computational complexity informs us about the difficulty of algorithms given specific computational primitives.
However, the question of which primitives we have access to when developing computing devices is a matter of physics (as quantum computing illustrates). This means that we can use empirical evidence about the physical world to justify or refute confidence in cryptography’s security. Today, the ultimate foundations of cryptography are formed by the combination of computational complexity results and empirical evidence about the world.
References
[1] Along the x, y, or z axes
[2] Without going into details, the message space is smaller than the set of all combinations of letters given that most of these combinations are meaningless. Meaningful messages are redundantly encoded.
[3] http://www14.in.tum.de/konferenzen/Jass05/courses/1/papers/gruber_paper.pdf
[4] The equation refers to the general case, but we can still use it to illustrate a particular case.
[5] To be precise, it’s that and the more general question of whether P=NP.