Although proposals have been made using other techniques, most common modern approaches to constructing secure voting systems can be divided into two categories: those based on homomorphic tallying (shorthand “homomorphic systems”) and those based on verifiable mixnets (shortand “mixnet systems”). Most systems, both prototypes in academia as well as production systems in industry, use one (or both) of these technologies to achieve the necessary properties for what is termed secure e-voting, and the related gold standard end-to-end verifiable voting.

Although proposals have been made using other techniques, most common modern approaches to constructing secure voting systems can be divided into two categories: those based on homomorphic tallying (shorthand “homomorphic systems”) and those based on verifiable mixnets (shortand “mixnet systems”). Most systems, both prototypes in academia as well as production systems in industry, use one (or both) of these technologies to achieve the necessary properties for what is termed secure e-voting, and the related gold standard end-to-end verifiable voting.
In this post we briefly describe the two approaches and then offer a qualitative pros & cons comparison of the two for aspects we have found significant in our experience evaluating and operating such systems. Given that Sequent’s voting system uses a mixnet as its core, it is unsurprising that our conclusion following the below comparisons leans in favour of that choice when building a secure voting system. However, at Sequent we’re open to the possibility of adding a homomorphic backend to our platform if careful analysis suggests it is desirable for particular use cases that may arise.
Homomorphic tallying
Voting systems based on homomorphic tallying exploit the homomorphic property of the underlying encryption to compute tallies. This homomorphic property makes it possible to add encrypted numbers together without decrypting them. The beauty of applying this technique to voting lies in the fact that when computing an election result we do not need to decrypt individual votes, only their sum, so that the secrecy of an individual’s ballot is preserved.
Unfortunately some technicalities have to be solved. We need a way to encode voter selections in a way that is amenable to this type of summing. This usually amounts to constructing vectors of ciphertexts for which a 1 represents a marked option on the ballot while a 0 represents an unmarked one, and then summing these vectors component-wise. In addition, because we only decrypt sums we also need a way to ensure that these encryptions represent valid choices. Not only because ballots could be nonsensical, but they could also be constructed maliciously to grant a voter more power than they ought to have. Preventing such cases is accomplished using zero knowledge proofs: using that technique we still don’t learn the contents of individual ballots but we are assured that they are valid.
You can learn more about the technical details of homomorphic tallying from any of the existing proposals featuring it in the literature, a prominent example is ElectionGuard.
Verifiable mixnets
Unlike homomorphic tallying, systems based on verifiable mixnets do decrypt individual ballots, but they do this after a process of anonymization which breaks the link between an encrypted ballot and the voter that cast it. The anonymization process amounts to a shuffling of a set of ballots such that the output set cannot be correlated with the input. The central problem that a verifiable mixnet solves is that of performing this shuffle while still ensuring that the output of that process corresponds to what went in, in other words, no manipulation took place. This is where, as above, zero knowledge proofs enter the picture, ensuring that the shuffling is correct while revealing no other information.
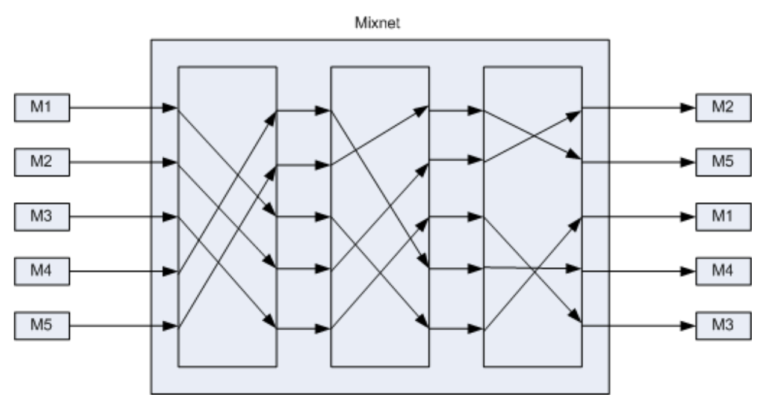
(A mixnet with three nodes, taken from here)
Verifiable mixnets come in different flavours, one example (we use at Sequent) is that of re-encryption mixnets. These implement the shuffle by permuting and re-encrypting the input ciphertexts such that the result is a shuffled set of ciphertexts that are equivalent but cannot be correlated with the input. Of course, whoever performs this shuffle does know the correspondence, but that’s where the “net” part of mixnet comes in. If this process is repeated by several independent parties, none of them will be able to trace the path of any ciphertext through the mix network: this will only be possible if all the independent parties pool their information together. So in effect, a mixnet implements a distribution of trust for the secrecy of the ballot, a recurring theme for secure voting systems.
You can learn more about all the technical details that we use at Sequent in these papers, and of course directly looking at our source code repository.
Comparison
Given this short description of the two techniques let’s take a look at some pros and cons of each for e-voting. We have divided the comparison into sections that are significant in our experience, in alphabetical order.
Generality
By generality we mean the degree to which the underlying cryptographic protocol can support a wide range of election and ballot types. Starting from the simplest election type, one which poses a yes/no question to voters, election and ballot types can increase in complexity up to schemes involving, for example, choosing one or more out of several choices, ordering of choices, scoring choices numerically, or even write-ins where voters can outright fill in a previously unspecified choice.
Generality is probably the axis along which homomorphic vs mixnet based voting systems differ most. As we mentioned before, a homomorphic tally system needs to convert voter’s ballots into suitable ciphertexts that can be summed exploiting the scheme’s homomorphic property. Unfortunately, beyond the case of choosing n-out-of-k options, this rules out the more complex examples we mentioned. Mixnets on the other hand can handle arbitrary ballot types, provided the ciphertext is sufficiently large to capture the ballot information. This makes generality a strong advantage of mixnet systems over homomorphic ones.
Implementation complexity
This category refers to the complexity of the software that makes up the voting systems. Absent other considerations, a higher implementation complexity is a negative factor in our comparison. One immediate reason is the higher difficulty in developing and maintaining the software that makes up the system. More importantly, a more complex implementation is more vulnerable to implementation errors and is harder to secure against both random errors and adversarial attacks.
In terms of total implementation complexity it is probably fair to say that a homomorphic system is less complex and wins out in this category. But this result leaves out important details as to where the complexity lies. Whereas mixnet systems pay a high complexity cost for the development of the shuffling and its proofs, homomorphic systems pay most of their complexity cost in ensuring that cast ballots are correctly constructed. This difference is a reflection of a key difference between the two. Homomorphic systems do not decrypt individual ballots and rely on complex proofs to certify that said ballots are valid. Mixnet systems however do decrypt after anonymization, so it is trivial in that case to remove invalid or maliciously constructed ballots.
The consequence of this difference is that homomorphic systems pay a large fraction of their complexity cost on the client where complex proofs must be constructed, and less so on the backend where the tally is more straightforward. Mixnets have the opposite complexity layout, the shuffle and tallying software is sophisticated, whereas the client is relatively simple. It could be argued that complexity on the client side is more problematic, since it is deployed in an uncontrolled environment, the user’s device, and is subject to greater degree of heterogeneity and uncertainty. Conversely, the backend runs in a controlled environment, the systems that specialised entities must run as trustees. In spite of this, we maintain that homomorphic systems come out ahead with respect to implementation complexity.
Performance
The discussion here draws parallels with the previous section, but replacing implementation complexity with computational complexity. Specifically, a homomorphic system requires more computation on the client side and less so on the backend. This occurs because these systems typically encrypt each possible selection with a ciphertext, resulting in vectors of ciphertexts that grow with the number of options presented to the voter. On top of this, zero knowledge proofs must be constructed for each of these encryptions. Both the encryption and the zero knowledge proofs add computational cost, a computation that takes place in the voter’s client which is limited in performance. On the other hand, once the ballots have reached the backend the necessary computation to verify them and perform the homomorphic sum is reduced, relative to the hardware characteristics available in a server environment..
Mixnet systems have the opposite layout. Ballot selections can usually be encoded into a single ciphertext, and proofs of validity are not essential as ciphertexts are decrypted after anonymization. However, the process of anonymization, the shuffle, is computationally intensive and grows in complexity the higher the degree of trust distribution is required. Depending on the techniques used, the size of the electorate and the hardware involved a tally can take up to hours in the worst cases.
Both homomorphic and mixnet based systems may encounter situations which make it a suboptimal choice. But while it is difficult to remedy cases in which client devices cannot be expected to compute large numbers of ciphertexts and proofs, it is usually easier to “throw hardware at the problem” on the backend. For this reason mixnets are more robust to demanding performance scenarios. However, when they can be applied, homomorphic systems show significantly better performance than mixnet systems in general.
Privacy
There are different degrees to which a voting system can be said to achieve privacy. The most common and basic requirement is ballot secrecy: the voting system does not reveal who voted for what. There are stronger notions of privacy such as receipt-freeness, where the voter cannot prove how they voted, and coercion resistance where the voter is able to cast their chosen vote even under the influence of a coercer.
Homomorphic and mixnet based e-voting systems have been the subject of academic research for decades in an attempt to satisfy these requirements. While many proposals exist that achieve ballot secrecy, receipt-freeness and coercion resistance are still an open problem. Our comparison with respect to privacy is then limited to ballot secrecy.
If constructed correctly (including choices for security parameters), and modulo implementation complexity aspects, both types of systems offer comparable ballot secrecy using cryptography that relies on well known hardness assumptions. In fact, in prominent instances of protocols of both kinds there is overlap in the cryptographic techniques with identical security properties, as is the case for example when using the ElGamal cryptosystem.
There are some considerations that escape a binary definition of ballot secrecy. One could argue that the tally counts are a form of leakage since they reveal more information than strictly the final result itself, a concern addressed by research into tally-hiding schemes. But this is true for both types of systems; homomorphic e-voting systems are not fully homomorphic, and are unable to perform arbitrary computations in ciphertext space to yield leak free results. In summary, we consider homomorphic and mixnet systems to be comparable with respect to privacy.
Verifiability
The gold standard for secure voting systems is end-to-end verifiability. A system is end-to-end verifiable if it is possible to certify that each of the key operations that make up an election (ballot casting, ballot recording and ballot counting) have been executed correctly. The question then becomes about whether homomorphic and mixnet systems can satisfy the requirements that make a system end-to-end verifiable.
Again, homomorphic and mixnet based e-voting systems have been the subject of academic research to satisfy these requirements. Within the category of end-to-end verifiability, there exist different proposals as to how each step of the verification takes place. One notable step is cast-as-intended verification, for which adequate usability is still an open problem. But whatever mechanisms are chosen to perform these verifications, they are generally equally applicable to both homomorphic and mixnet systems.
We can say that, if constructed correctly, both types of systems achieve comparable levels of verifiability; there are many examples of both types in the academic literature on end-to-end verifiable systems. Helios in particular is a system that has been proposed in both homomorphic and mixnet variants. In summary, we consider homomorphic and mixnet based systems to be comparable with respect to verifiability.
Conclusion
One would think that the conclusion of our qualitative comparison between homomorphic and mixnet based systems would favour the former, given that it edges out its mixnet counterpart in more of the categories above. However, this advantage only manifests in the concrete cases where homomorphic systems can be applied at all. In contrast, mixnets can handle a much wider range of scenarios, albeit at a higher complexity cost. If one requires a system for a particular use case which does not rule out homomorphic based systems, they are better. But if one wants a future proof system that can be relied upon in general, mixnets are a better choice.