This article demonstrates the natural extension of Diaz’s 2002 degree of anonymity model to voting scenarios. The outcome is straightforward but holds potential value for intricate cases like weighted voting, where privacy concerns surpass the conventional “bisimilarity-under-swapping” definition outlined by Delaune in 2009. These concerns arise from the possibility of information leakage through election results, as highlighted in Delaune’s work:

This article demonstrates the natural extension of Diaz’s 2002 degree of anonymity model to voting scenarios. The outcome is straightforward but holds potential value for intricate cases like weighted voting, where privacy concerns surpass the conventional “bisimilarity-under-swapping” definition outlined by Delaune in 2009. These concerns arise from the possibility of information leakage through election results, as highlighted in Delaune’s work:
It is important to note that the definition of “bisimilarity-under-swapping” remains resilient even in scenarios where the outcome of the election necessitates the disclosure of votes from VA and VB. This applies to situations such as unanimous voting or when other voters reveal their choices, leading to the deduction of votes for VA and VB.
The notion that information can potentially leak from voting results directs our attention to the degree of anonymity model. This model, rooted in information theory, enables the quantification of anonymity provided by anonymous connection schemes. It considers attackers who gather probabilistic information about users. Unlike the standard possibilistic privacy definition for voting, the degree of information in this model pertains to probabilistic inference. The measure is not binary; instead, it quantifies the amount of information an attacker can obtain by observing the process. In the context of voting, as discussed later, the attacker acquires information by observing the results, which are accessible regardless of the existence of ballot privacy.
By quantifying information gain, entropy naturally results (Diaz 2009).

As a measure of degree of anonymity, the authors apply a normalization factor based on maximum entropy (zero information leakage):

Given the normalization

Extension to Voting
Using the degree of anonymity model, we can determine who sent a message out of possible groups (the anonymity set). This model should be extended to the case of voting, where the attacker wants to determine the voter’s choice. The availability of individual votes as plaintexts varies depending on the secure voting scheme employed. Consequently, the translation between different scenarios is not instantaneous. In one case, the focus is on determining a single variable out of n options, while in the context of voting, the objective is to ascertain vote choices based on election results.
However, it is possible to incorporate probabilities directly into the degree of anonymity model. These probabilities should be derived from the election results, as they constitute the publicly available information accessible to the attacker. Furthermore, it is desirable to establish a general approach that does not rely on the specific electoral method or the format of the election result. We start with:
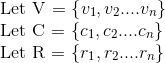
These are sets of voters, choices and election results.
The function ‘a’ represents the individual voter’s selection, defined as a mapping that associates each voter with their respective choice. On the other hand, the function ‘t’ denotes the election tally, which maps the set of choices made by voters to the corresponding result.
Ar corresponds to the set of all functions ‘a’ that generate the outcome ‘r’, representing the sets of selections made by voters. Expanding on this, the function ‘m’ denotes the count of distinct functions ‘a’ in which voter ‘v’ selects choice ‘c’ and the overall result is ‘r’. In essence, it quantifies the number of instances where voter ‘v’ chooses ‘c’ and the final result corresponds to ‘r’.
These expressions allow us to provide equivalent expressions for the terms in the original definition of degree of anonymity. According to the election result, the entropy corresponding to the uncertainty of a voter’s choice is
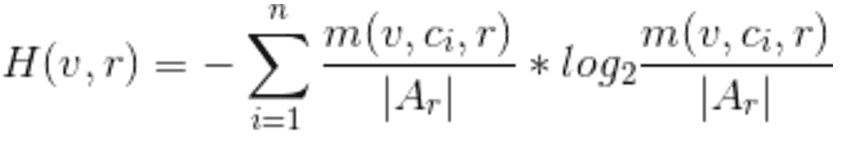
In this case, entropy is simply the standard expression for entropy, but with probabilities that correspond to the likelihood that a certain choice will be selected given a certain election result. When there is no information about the election, the maximum entropy corresponds to a uniform probability distribution for the voter’s choice, resulting in
where |C| is the number of choices (the cardinality of C). Finally, the degree of privacy is
which quantifies the degree to which a voter’s v choice remains secret given the election result r. This expression exhibits similarities to the degree of anonymity model, albeit with certain modifications. Firstly, we are addressing the degree of privacy, quantifying the level of knowledge about a voter’s choice, rather than attempting to de-anonymize the sender of a message. Furthermore, this result pertains to each individual voter. While this characteristic may not always be relevant, it holds significance in scenarios involving weighted voting, where voters possess distinct degrees of anonymity. Additionally, it is possible to derive aggregate values, such as the average or minimum degree of anonymity. Another generalization involves computing expectation values over results for a given setup. As an extreme example, in an election with a single voter, the degree of anonymity would always be 0, regardless of the result.
As mentioned previously, the aforementioned definition applies universally to any election, regardless of the electoral method, result type, or even the design of the ballot. Now, let’s delve into some specific examples to further illustrate this point.
Examples
We calculate values for examples. In all cases we are using a plurality rule for the function t: V => C => R.
Yes/No vote, Single voter
This is a Yes/No vote (ballot options are Yes or No). We have a single voter, John.
V = { John }, C = { Yes, No }, R = { {Yes:1, No:0}, {Yes:0, No:1} }
In the following expression:
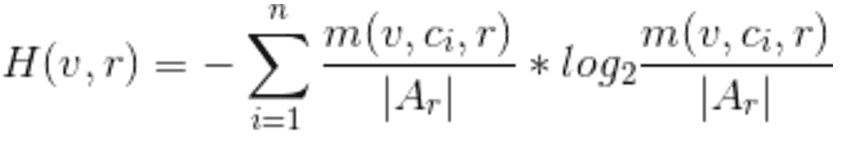
The value of n is 2, for two possible results (the cardinality of C). Consider the case where r = Yes, then
Ar = { (John, Yes) }, and |Ar| = 1
since it is the only way that John could have voted. Similarly,
m(John, Yes, Yes) = 1 and m(John, No, Yes) = 0
again, for the same reason. The entropy then reduces to
H(v, r) = 1/1*log(1/1) = 0
which when plugged into
gives
d(John, Yes) = d(John, No) = 0
The degree of anonymity is zero. This matches the obvious fact that in an election with a single voter, their vote will be revealed.
Yes/No vote, Unanimous result
V = { v1 … vn }, C = { Yes, No }, R = { {Yes:n, No:0}, {Yes:0, No:n} }
In the following expression:
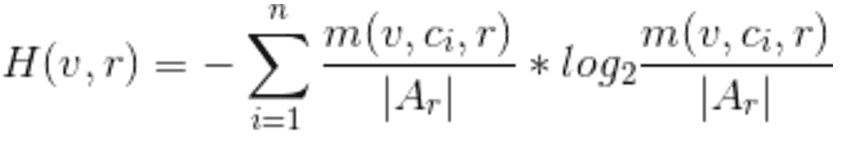
we see that the unanimous vote case has a similar form as the case of a single voter, except for a general number of voters and results:
|Ar| = 1
for all r, and also
m(v, Yes, {Yes:0, No: 10} ) = 0 and m(v, Yes, {Yes:10, No: 0} ) = 1
which leads to
d(v, r) = 0
for all v and r. Once again, this matches the obvious expectation: in a unanimous election, all votes are disclosed.
Yes/No vote, General case
V = { v1 … vn }, C = { Yes, No }, R = { {Yes:n, No:0} … {Yes:0, No:n} }
In this case, the cardinality of R is |C|, as we are not confining the results solely to unanimous outcomes. The calculation for |Ar| and m deviates from the previous approach. By indexing the results in R based on the number of positive votes, we obtain the following:
with a binomial coefficient on the right. This is the number of ways it is possible to obtain the result r. We also have
dividing the previous two expressions provides
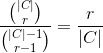
Because this is a Yes/No election
which when divided by |Ar|
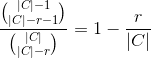
The complete expression for H is therefore
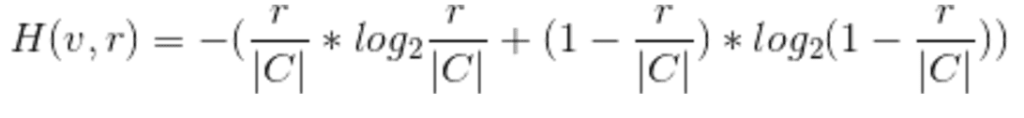
at this point, we can do a couple of sanity checks. Firstly, the probabilities in the entropy expression (r/|C| + 1 — r/|C|) sum to 1. Secondly, these examples highlight a common-sense inference. If an election comprises |C| choices and the number of “Yes” votes is r, then the probability of any voter selecting “Yes” must be r / |C|. Although our generalized approach for calculating entropy is more extensive than our intuition for indistinguishable voters under the plurality rule, it aligns with logical reasoning.
Finally, the degree of privacy for the general Yes/No election is
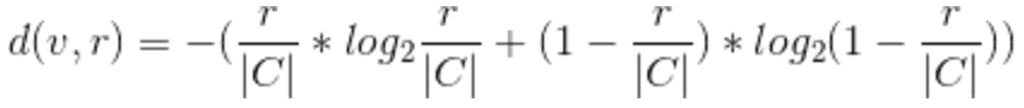
Below is a graph of this function for a fixed value of 10 voters (|C| = 10).
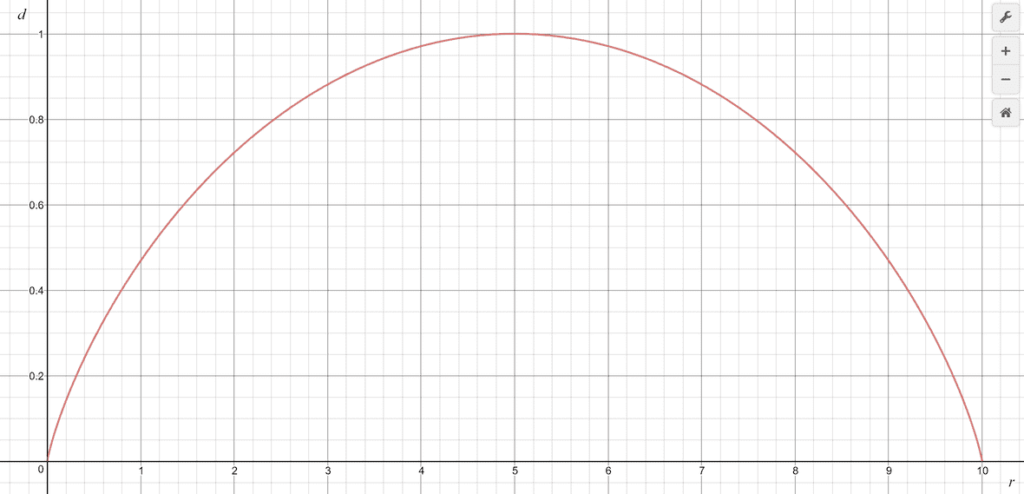
As we saw in the previous section, unanimous elections correspond to the two edges of the graph, where d = 0.
Summary
The application of the generalized degree of anonymity model in the context of voting has demonstrated its versatility and relevance. This extension proves applicable to diverse voting methods, providing a flexible approach. Through simple yet illustrative examples, we observe that the model’s calculations align with outcomes derived from traditional methods specific to each type of election. While these initial examples may seem straightforward, the significance of the degree of privacy becomes particularly apparent in more complex scenarios where voters are distinguishable, and results may inadvertently reveal additional information. Weighted voting serves as a prime illustration of such cases. While the definitions presented herein can be equally applied to this scenario, employing them in their general form may require additional considerations to address potential combinatorial challenges.
References
Diaz 2002 — Towards measuring anonymity
Delaune 2009 — Verifying privacy-type properties of electronic voting protocols
[3] It is also possible to use a non-uniform prior probability here. In that case the resulting conditional probabilities must be derived in such a way that relative magnitudes are preserved.