In cryptography, ElGamal is an asymmetric cryptosystem in which public and private keys are used to encrypt communication between two parties.
ElGamal encryption plays a similar role to the more commonly known RSA and is easily adaptable to a variety of cryptographic groups, and is semantically secure provided that the DDH assumption holds. In the case of internet voting, ElGamal is usually instantiated over a multiplicative subgroup induced by a safe prime. This requires that plaintext data must be first encoded into this subgroup before it can be encrypted.

In cryptography, ElGamal is an asymmetric cryptosystem in which public and private keys are used to encrypt communication between two parties.
ElGamal encryption plays a similar role to the more commonly known RSA and is easily adaptable to a variety of cryptographic groups, and is semantically secure provided that the DDH assumption holds. In the case of internet voting, ElGamal is usually instantiated over a multiplicative subgroup induced by a safe prime. This requires that plaintext data must be first encoded into this subgroup before it can be encrypted.
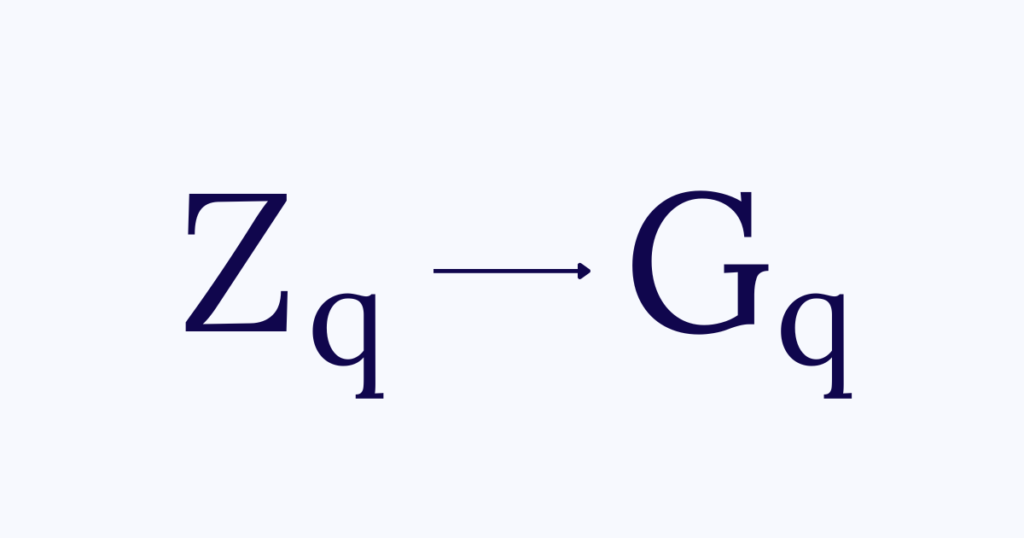
To ensure ballot privacy, the Sequent voting system uses an ElGamal re-encryption mixnet. As mentioned above, protected data must first be encoded into the plaintext space in which ElGamal operates. The information can be encrypted once it has been encoded in this space. During decryption, the ciphertexts are decrypted first, and then the plaintexts are encoded back into the original data.
ElGamal’s plaintext (and ciphertext) space is a multiplicative subgroup Gq, for some choice of p, a safe prime modulus such that p = 2q + 1. In order to encode data, first convert it into an integer (a universal data type that can hold any information), and then map it into Gq. In a single ciphertext, the number of integers that can be encoded is determined by the order q of Gq, so we can map numbers from Zq into Gq.
As I couldn’t find any references describing this simple procedure well, I decided to write it myself.
Encoding With the Legendre Symbol
One reference we can find is this from Advances in Cryptology — EUROCRYPT 2017.

To begin with, when using a safe prime p = 2q + 1, the multiplicative subgroup Gq is the set of quadratic residues mod p, which makes the scheme semantically secure. Accordingly, we should use the simple m x (m/p) encoding procedure. But why is (m/p) x m guaranteed to be a quadratic residue? The reference contains hints, which we expand on below.
Step 1: the legendre symbol is defined as
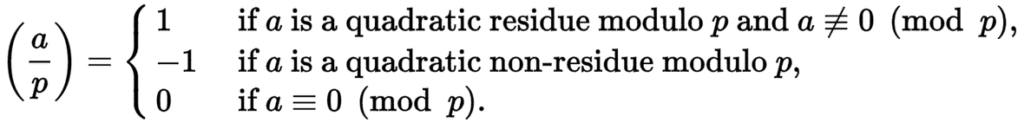
When the input integers range from q to p, then there are only two possibilities for encoding.
The expression (m/p) x m reduces to leaving m unchanged (1 x m) or reversing its sign (-1 x m). In particular, if m is already a residue, then (m/p) x m is still a residue since (1 x m) = m.
Step 2: we have that
Step 3: the first supplement of the law of quadratic reciprocity states
since p is a prime, then p mod 4 has only two possible values (1 and 3), so
if p ≡ 3 (mod 4) then -1 is a nonresidue modulo p
Step 4: our modulus p is a safe prime p = 2q + 1, where q is also a prime. Meaning:
q = 1 mod 4 or q = 3 mod 4
Expanding each case[1]
*q = 1 mod 4 ⇒ **2q = 2 mod 4 ⇒ **2q + 1 = 3 mod 4 ⇒ *p = 3 mod 4
similarly
q = 3 mod 4 ⇒ 2q 4 = 6 mod 4 ⇒ 2q = 2 mod 4 ⇒ p = 3 mod 4
Therefore in both cases, for a safe prime p, we have
p = 3 mod 4
Now, in reverse order, we combine each of the previous four steps. By the step 4 we have:
p = 3 mod 4
which by step 3 implies that
-1 is a nonresidue modulo p
which by step 2 implies that
(-1 x m) is a residue if m is not a residue
which by step 1 implies that
(m/p) x m is a residue if m is not a residue
Also by step 1 we saw that
(m/p) x m = 1 x m is a residue if m is a residue
Therefore in all cases
(m/p) x m is a quadratic residue modulo p for a safe prime p = 2q + 1
which is what we set out to prove.
Helios and Univote Example Code
Using ElGamal encryption, let’s take a look at two open source e-voting projects, Helios by Ben Adida and UniVote by the Bern E-voting group. Due to the fact that the voting booth runs in the browser, the code is written in JavaScript. The ElGamal encoding of integers is found in Helios’ elgamal.jsfile, which is also included in Sequent’s voting booth.
var y = m.add(BigInt.ONE);
var test = y.modPow(pk.q, pk.p);
if (test.equals(BigInt.ONE)) {
this.m = y;
} else {
this.m = y.negate().mod(pk.p);
}
Due to the fact that the subgroup Gq does not include the value zero, the first line adds one to the input. Following these lines are the implementations of (m/p) x m encoding. As you may recall, the legendre symbol can take on either a value of 1 or a value of -1. In the case (1 x m), the first branch of the if statement leaves m unchanged. This second branch corresponds to changing the sign of m, the (-1 x m) case. Calculation of the legendre symbol is based on Euler’s criterion in the if statement
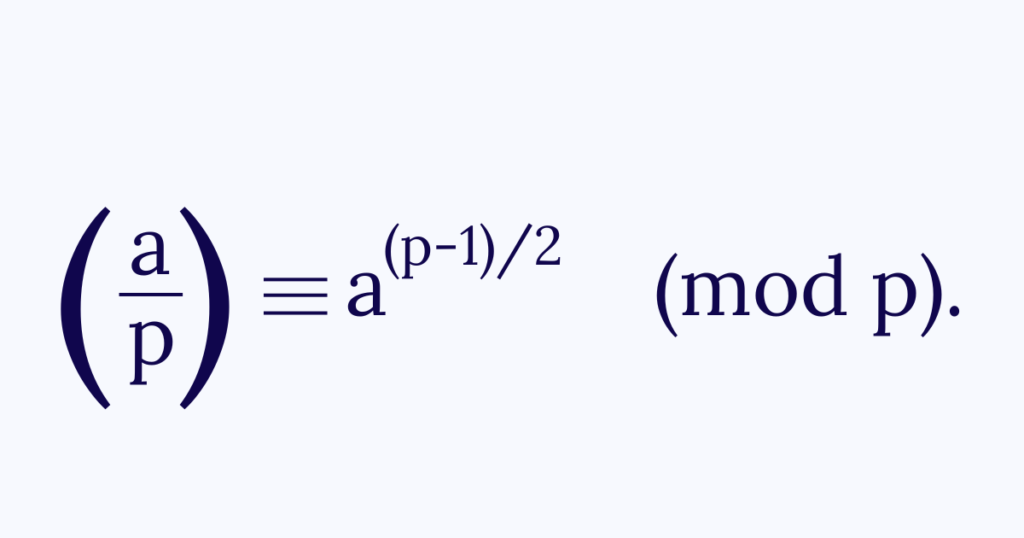
This shows that the javascript code is in effect calculating (m/p) * m. We can see a similar method in UniVote, the code is found here:
var one = leemon.str2bigInt("1", 2, 1);
var t1 = leemon.add(bigIntInZq, one);
var t2 = leemon.powMod(t1,
encryptionSetting.q, encryptionSetting.p);
if (leemon.equals(t2, one) == 1) {
return t1;
} else {
return leemon.sub(encryptionSetting.p, t1);
}
As before, we’re adding 1 and then branching according to Euler’s criterion. Unlike above, in this case we have the value p – m instead of (1 x m). Since modular congruence can be achieved by subtraction[2], then this can be done.
-m mod p = (0 — m) mod p = p — m mod p
So both expressions, -m and p — m are equivalent, mapping the input m to quadratic residue.
Example Values
Here we show some concrete encoding examples for small p. Let’s first print the values in G5 for a choice of safe prime 11 = (2 x 5) + 1.

The quadratic residues are thus G5 = {1, 3, 4, 5, 9}. Now let’s see if the encoded in the allowed range q=5 actually map to residues.
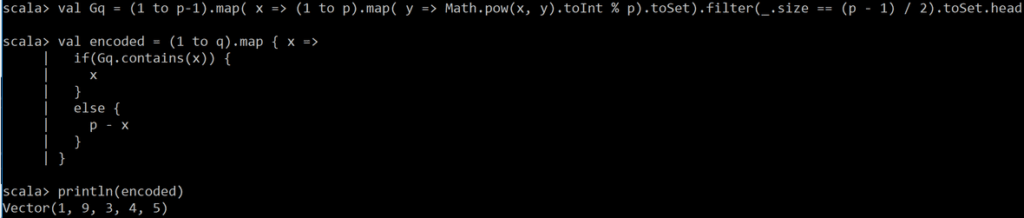
where we can see that the encoded values are indeed in G5. Let’s run another test for p = (2 x 11) + 1
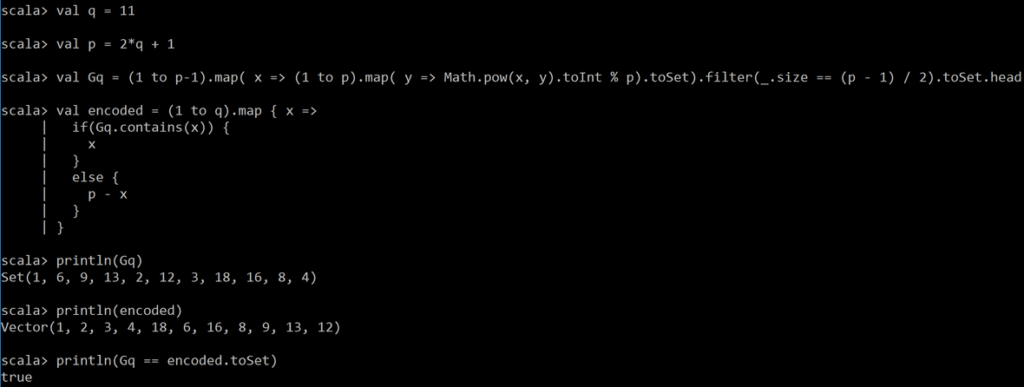
Again, the encoding works.
In Summary
In this post we learned how ElGamal encrypts data by encoding it into the correct subgroup with the expression (m/p) x p, expressed as the legendre symbol. The properties of modular arithmetic also explain why this works. The Euler criterion was used to determine residuosity in two implementations of this technique. Last but not least, we examined some examples of subgroups and encodings for small p and q values.
References
[1] We are using two properties here
- if a = b mod n, then k a = k b (mod n) for any integer k (compatibility with scaling)
- if a* = b mod n, a1 + *a2 ≡ b1 + b2 (mod n) (compatibility with addition)
[2] Compatibility with subtraction,
if a1 = b1 mod n and a2 = b2 mod n, *then a1 — *a2 = b1 — b2 (mod n) (compatibility with subtraction)